Как не ошибиться, рассчитывая среднюю доходность инвестиций, что такое «подножка волатильности», и почему умелая диверсификация не только обеспечивает стабильность инвестиционного портфеля, но и улучшает доходность.
Все инвесторы сталкиваются с необходимостью расчета средней доходности своего портфеля. Это нужно для того чтобы прогнозировать его будущую стоимость. Без такого прогноза невозможно, например, решить, на какую сумму следует пополнять инвестиционный портфель, чтобы достичь поставленных целей к сроку.
Часто инвесторы ошибаются в расчетах, потому что используют неправильную формулу. Использовать ошибочную оценку в планировании будущих действий опасно. Ценой просчета может стать качество жизни в старости или образование ребенка.
Как правильно оценить среднюю доходность
Среднюю доходность портфеля в заданном периоде нужно считать не как среднюю арифметическую, а как среднюю геометрическую. Разберемся на простом примере.
Допустим инвестор вкладывает деньги в российские акции через фонд А и российские облиции через фонд Б в пропорциях 60 на 40. Ниже в таблице приведены данные по ежегодной динамике стоимости акций, облигаций и совокупного портфеля.
Таблица №1. Доходности фондов А, Б и портфеля 60/40 за 4 года (в руб).
| Инструмент | 2016 | 2017 | 2018 | 2019 |
|---|---|---|---|---|
| Фонд А | 28,67% | -2,22% | 16,74% | 37,44% |
| Фонд Б | 15,24% | 14,83% | 2,7% | 15,34% |
| Портфель 60/40 | 23,30% | 4,60% | 11,12% | 28,60% |
Источник: Bloomberg, расчеты FinEx
Акции, облигации и портфель за все время принесли 101,86%, 56,74% и 83,81%. На первый взгляд получается 20,16%, 12% и 16,9% в среднем за год. На самом же деле эти цифры завышены. Как так вышло? Дело в том, что арифметическая средняя (сумма доходностей, поделенная на количество периодов) не походит для расчета инвестиционных результатов, так как доходность, полученная в очередном периоде, относится к стоимости портфеля в предыдущем периоде, и включает доходность на доходность прошлого периода, а не только на сумму инвестиций. Например, если портфель упал на 5% за период с уровня 10000, а затем поднялся на 5%, он не вернется к 10000, а будет стоить 9975 руб. В этом примере разница небольшая, но чем больше рыночная нестабильность, то тем больше будет расхождение. — это прекрасно видно на примере фонда А, который является более волатильным, чем фонд Б.
Для того, чтобы правильно учесть волатильность доходностей и их влияние на результат используют среднюю геометрическую или, как еще её называют, аннуализированную доходность (Compound Average Growth Rate). Она рассчитывается как корень степени n из произведения доходностей за n периодов. Например, ∜(1,232 * 1,046 * 1,1112 * 1,286) даст среднюю доходность портфеля в 16,5% в год (а не 16,7%, как средняя арифметическая). Как и средняя арифметическая, средняя геометрическая не всегда соответствует показателю в каждый конкретный год, но при этом в конце периода она трансформирует первоначально инвестированную сумму в точный итоговый результат инвестирования. Как следствие, именно этот показатель, а не среднюю арифметическую доходность стоит использовать для долгосрочного инвестиционного планирования. Сравнение динамики средней арифметической и реальной доходностей представлены в таблице №2 и на графике №1.
График №1. Динамика средней арифметической и реальной стоимости портфеля (в руб).
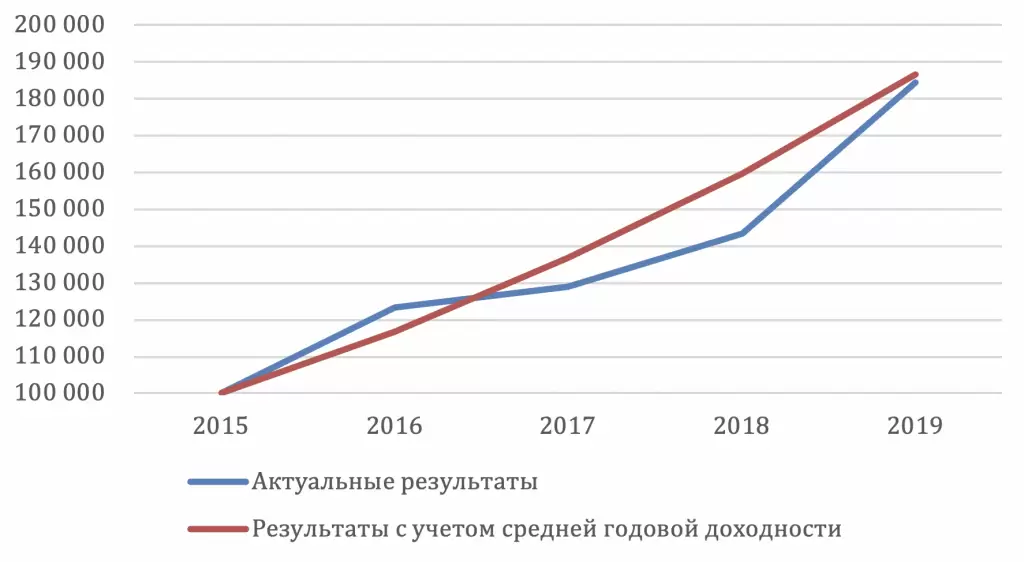
Таблица №2. Динамика средней арифметической и реальной стоимости портфеля (в руб).

Источник: Bloomberg, расчеты FinEx
Что такое подножка волатильности?
Разницу между средней арифметической и средней геометрической доходностью в академических кругах называют «volatility drag» или «подножка волатильности». Почему же речь идет о «подножке»? Потому что с точки зрения математики, чем более волатилен ряд доходностей, тем сильнее геометрическая доходность будет отставать от арифметической.
Volatility Drag = средняя арифметическая доходность - средняя геометрическая доходность
Несмотря на свою простоту, это формула позволяет сделать ряд интересных выводов — например, относительно опасности популярных у многих инвесторов инвестиций с использованием заемных средств («финансового рычага»). Когда инвестор рискует не только собственными средствами, но и занимает дополнительные деньги у своего брокера для того, чтобы увеличить размер своего портфеля, он увеличивает и его волатильность.
Например, использование рычага 2 (на каждый вложенный собственный рубль инвестиций инвестор получает в кредит еще один рубль и инвестирует его в рынок) обеспечивает удвоение арифметической доходности (без учета расходов в связи с использованием рычага). Но в случае падения, удваиваются и потери. В результате из-за бремени волатильности средняя геометрическая доходность меняется медленнее.
Как диверсификация отражается на волатильности портфеля?
Диверсификация портфеля сокращает volatility drag и поэтому положительно сказывается на доходности портфеля. Рассмотрим простой пример: инвестор может инвестировать в акции компании А или в акции компании А и Б. Волатильность акций компании А 26%, Б – 11%, их годовые доходности и результаты инвестирования для первого и второго случая представлены в таблице ниже. Как видно из таблицы, из-за большей волатильности первого инструмента, даже большие номинальные доходности несут в итоге результат хуже, чем в случае с инвестированием в разные инструменты даже пусть с меньшей общей доходностью. Это происходит как раз из-за того, что волатильность съедает большую доходность. Во втором случае портфель падает меньше чем при инвестировании исключительно в акции А, и даже небольшая доходность дает лучший итоговый результат в 6,7% за 10 лет.
График №2. Динамика портфеля только из акций компании А и портфеля из акций компаний А и Б в пропорции 50/50 (в руб).
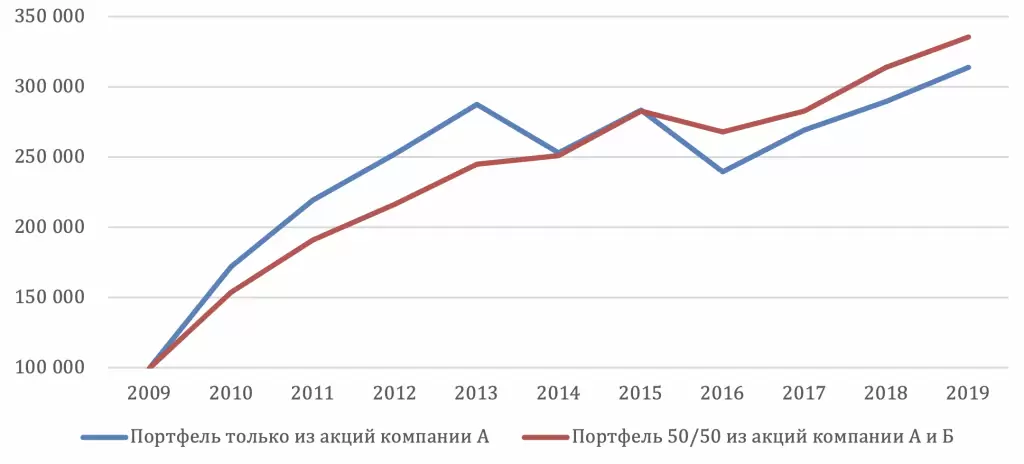
Источник: Bloomberg, расчеты FinEx
Таблица №3. Динамика портфеля только из акций компании А и портфеля из акций компаний А и Б в пропорции 50/50 (в руб).
.webp)
Источник: Bloomberg, расчеты FinEx






